16 Mar 2018 |
deep-learning |
循环神经网络(RNN)与普通的神经网络相比,循环神经网络能够记住上一次的信息,就是在隐藏层输入的时候,不仅仅接受来自与x的输入,还接受来自于上一次隐藏层的值。
常见的RNN示意图:
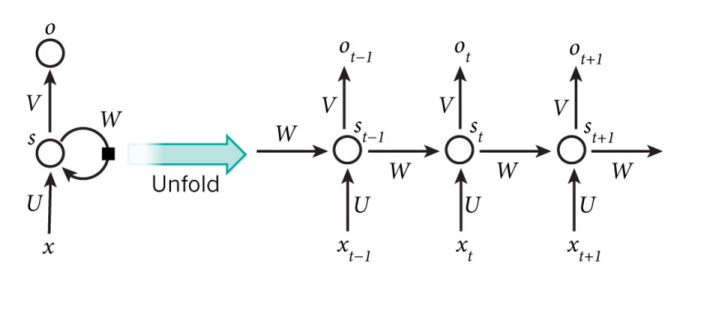
其中的U是输入与隐藏层之间的权重矩阵,W是隐藏层以隐藏层之间的权重矩阵,V是隐藏层与输出层之间的权重矩阵。
一个标准的RNN模型如图所示:
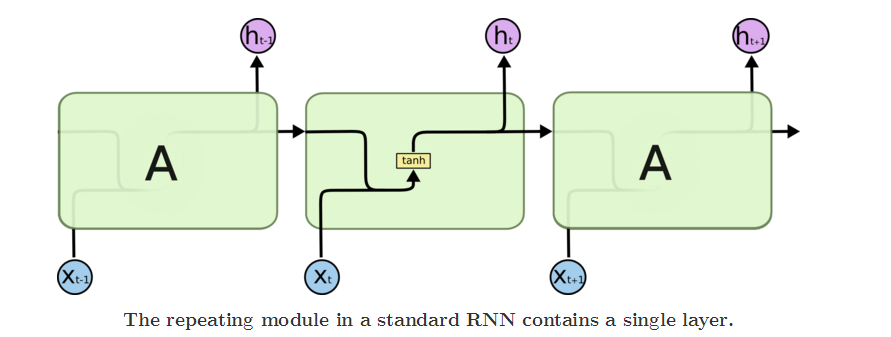
主要计算入下:
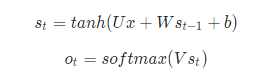
为了更好的理解执行过程,我画了一个RNN前向传播的流程执行图。首先输入经过嵌入层embed,然后再经过隐藏层,隐藏层输入当前的状态值s_t,然后再经过softmax输出。


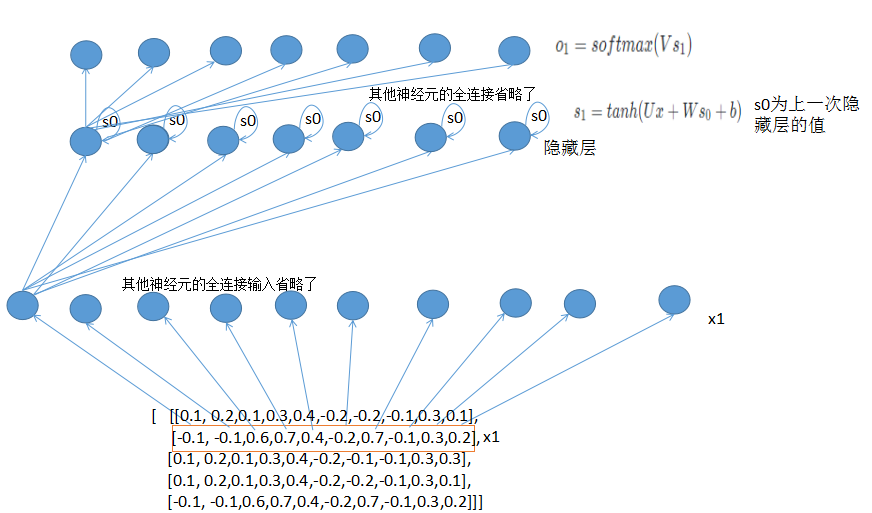
RNN前向传播的代码:
def forward_propagation(self, x):
# The total number of time steps
T = len(x) #输入的总长度
# During forward propagation we save all hidden states in s because need them later.
# We add one additional element for the initial hidden, which we set to 0
s = np.zeros((T + 1, self.hidden_dim))
s[-1] = np.zeros(self.hidden_dim)#初始化隐藏层的值,一般为0
# The outputs at each time step. Again, we save them for later.
o = np.zeros((T, self.word_dim))
# For each time step...
for t in np.arange(T):
# Note that we are indxing U by x[t]. This is the same as multiplying U with a one-hot vector.
s[t] = np.tanh(self.U[:,x[t]] + self.W.dot(s[t-1]))#每次隐藏层的输入包括当前x的输入和上一次隐藏层的值
o[t] = softmax(self.V.dot(s[t]))#隐藏层经过全连接和softmax层后输出
return [o, s]
更好的博文请参考:
Recurrent Neural Networks Tutorial, Part 2 – Implementing a RNN with Python, Numpy and Theano
Understanding LSTM Networks
The Unreasonable Effectiveness of Recurrent Neural Networks
上面的文章写的真的很棒哦~
11 Mar 2018 |
deep-learning |
卷积神经网络:在空间上共享参数的网络,用共享权重的卷积层替换了一般的全连接层。(假设在一张图片中要识别出其中的猫,不管猫在图片的任何位置,都可以使用相同的权重去寻找猫。当我们试图识别一个猫的图片的时候,我们并不在意猫出现在哪个位置。无论是左上角,右下角,它在你眼里都是一只猫。我们希望 CNNs 能够无差别的识别,这如何做到呢?如我们之前所见,一个给定的 patch 的分类,是由 patch 对应的权重和偏置项决定的。
如果我们想让左上角的猫与右下角的猫以同样的方式被识别,他们的权重和偏置项需要一样,这样他们才能以同一种方法识别。
这正是我们在 CNNs 中做的。)
CNN 的学习方式:它学习识别基本的直线,曲线,然后是形状,点块,然后是图片中更复杂的物体。最终 CNN 分类器把这些大的,复杂的物体综合起来识别图片。CNN 是自主学习。
滤波器滑动的间隔被称作 stride(步长)。这是你可以调节的一个超参数。增大 stride 值后,会减少每层总 patch 数量,因此也减小了模型大小。通常这也会降低图像精度。
卷积层滤波器的数量被称为滤波器深度
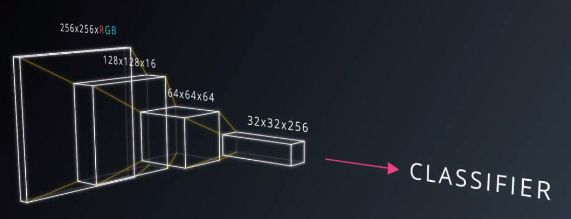
维度
综合目前所学的知识,我们应该如何计算 CNN 中每一层神经元的数量呢?
输入层(input layer)维度值为W, 滤波器(filter)的维度值为 F (height * width * depth), stride 的数值为 S, padding 的数值为 P, 下一层的维度值可用如下公式表示: (W−F+2P)/S+1。 滤波器的数量就是下一层的深度(相当于每个滤波器扫描一次得到一层)。
TensorFlow 使用如下等式计算 SAME 、PADDING
SAME Padding, 输出的高和宽,计算如下:
out_height = ceil(float(in_height) / float(strides[1]))
out_width = ceil(float(in_width) / float(strides[2]))
VALID Padding, 输出的高和宽,计算如下:
out_height = ceil(float(in_height - filter_height + 1) / float(strides[1]))
out_width = ceil(float(in_width - filter_width + 1) / float(strides[2]))
最大池化
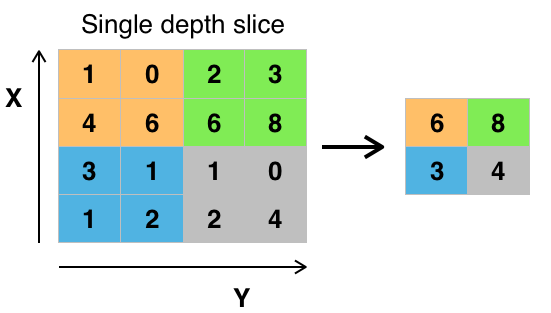 例如 [[1, 0], [4, 6]] 生成 6,因为 6 是这4个数字中最大的。同理 [[2, 3], [6, 8]] 生成 8。 理论上,最大池化操作的好处是减小输入大小(这样也会避免过拟合),使得神经网络能够专注于最重要的元素。最大池化只取覆盖区域中的最大值,其它的值都丢弃。
近期,池化层并不是很受青睐。部分原因是:
例如 [[1, 0], [4, 6]] 生成 6,因为 6 是这4个数字中最大的。同理 [[2, 3], [6, 8]] 生成 8。 理论上,最大池化操作的好处是减小输入大小(这样也会避免过拟合),使得神经网络能够专注于最重要的元素。最大池化只取覆盖区域中的最大值,其它的值都丢弃。
近期,池化层并不是很受青睐。部分原因是:
- 现在的数据集又大又复杂,我们更关心欠拟合问题。
- Dropout 是一个更好的正则化方法。
- 池化导致信息损失。想想最大池化的例子,n 个数字中我们只保留最大的,把余下的 n-1 完全舍弃了。
卷积过程可视化
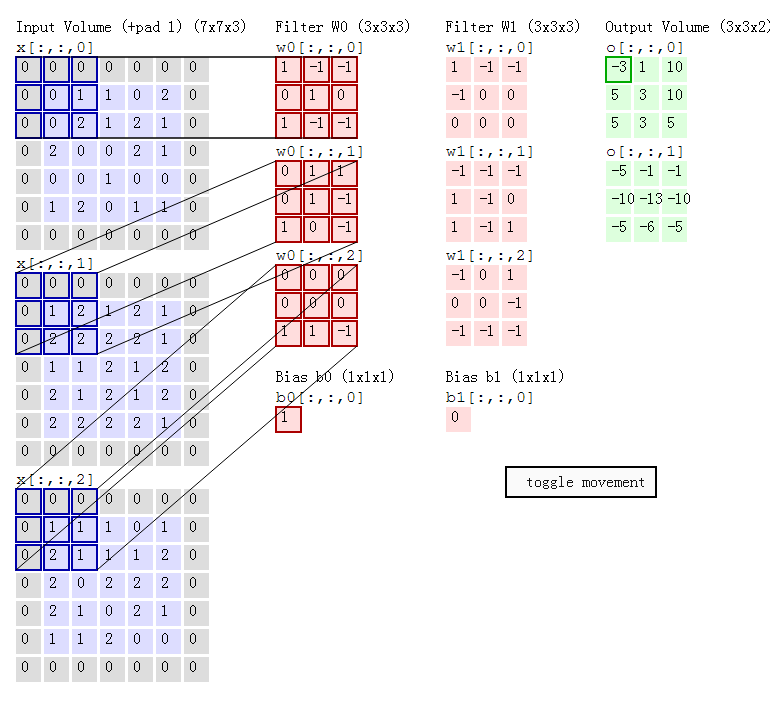
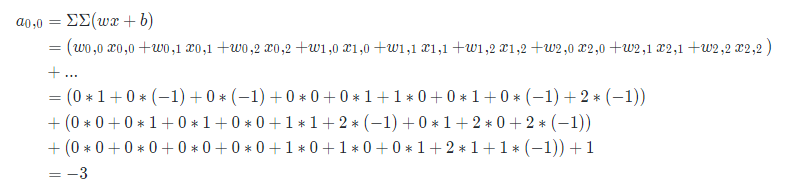
04 Mar 2018 |
deep-learning |
现在,我将简单复习下梯度下降概念,使我们能够开始用 MiniFlow 训练我们的网络。注意,我们的目标是通过尽量减小代价,使我们的网络输出与目标值尽量接近。你可以将代价看做一座山,我们想要到达山底。
想象你的模型参数表示为一个停在山顶的球。直观地来说,我们希望将球推下山。这样可以明白,但是我们讨论的是代价函数,如何知道哪条路是下山呢?
幸运的是,梯度下降正好给出了这一信息。
严格来说,梯度实际上指的是上坡,是最陡上升方向。但是,如果我们在此值前面加个负号,就得出了最陡下降方向,这正是我们需要的。
稍后你将详细了解梯度,但是暂时可以将其看做数字向量。每个数字表示我们应该对照着调整神经网络中相应的权重或偏置的数量。按照梯度值调整所有的权重和偏置降低了网络的代价(或误差)。
听明白了吗?
好的!现在我们知道朝着哪个方向推球了。下一步是考虑用多大的推力,称之为学习速度,该名称比较恰当,因为该值确定了神经网络学习的快慢速度。
你可能希望设置非常大的学习速度,这一网络就能学的非常快,对吧?
要小心!如果该值太大,可能会迭代过度并最终偏离目标。
 收敛这是理想行为
收敛这是理想行为
 发散-学习速率过高会出现这种情况
发散-学习速率过高会出现这种情况
那么,什么样的学习速度合适呢?
我们只能做出猜测,根据以往经验,0.1 至 0.0001 范围的值效果最好。0.001 至 0.0001 范围的值很常见,因为 0.1 和 0.01 有时候过大。
下面是梯度下降的公式(伪代码):
x = x - learning_rate * gradient_of_x
x 是神经网络使用的参数(即单个权重或偏置)。
我们将 gradient_of_x(上坡方向)与 learning_rate(推力)相乘,然后将 x 减去相乘结果,从而向下推动。
太棒了!