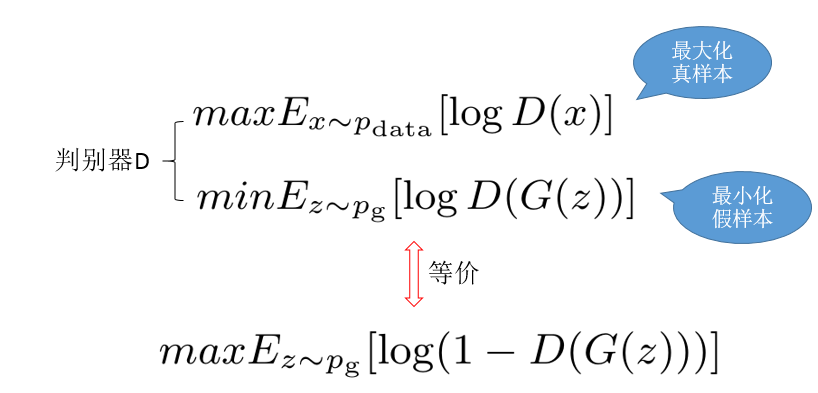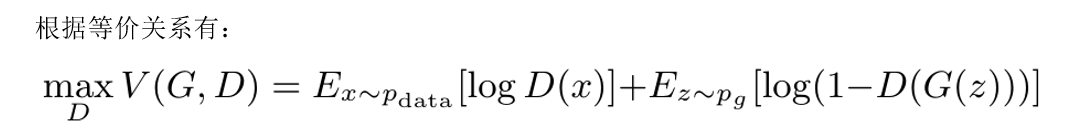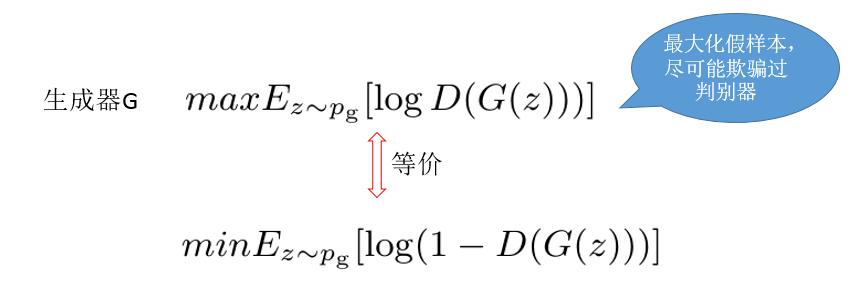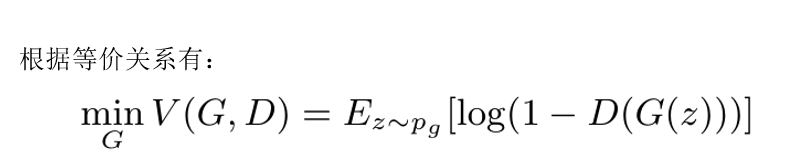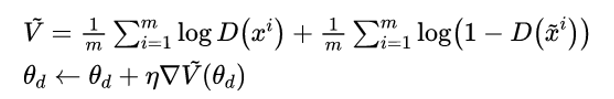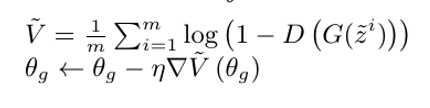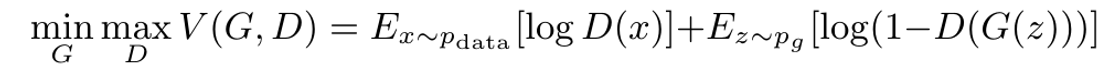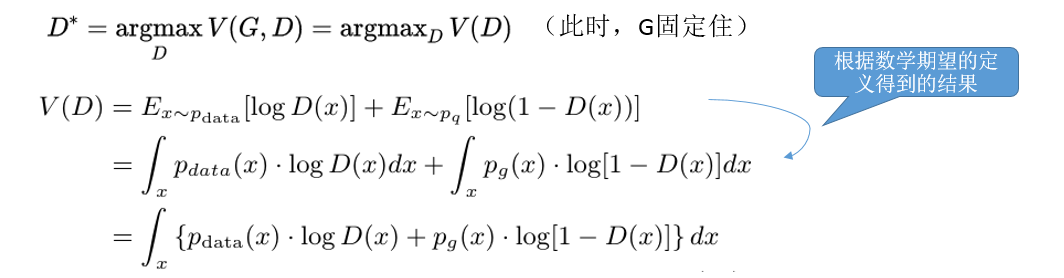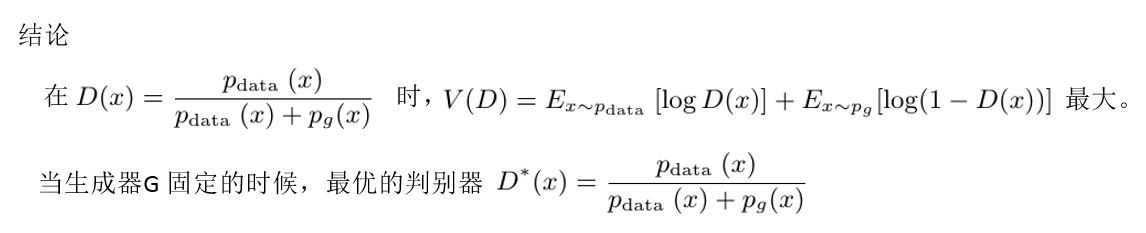26 Jun 2019 |
deep-learning |
GAN(Generative Adversarial Network):生成对抗网络。
核心思想
目标函数
判别器目标函数
- 判别器的目标就是区分真假样本,其实就是一个二分类,所以它的目标函数就是如下形式:
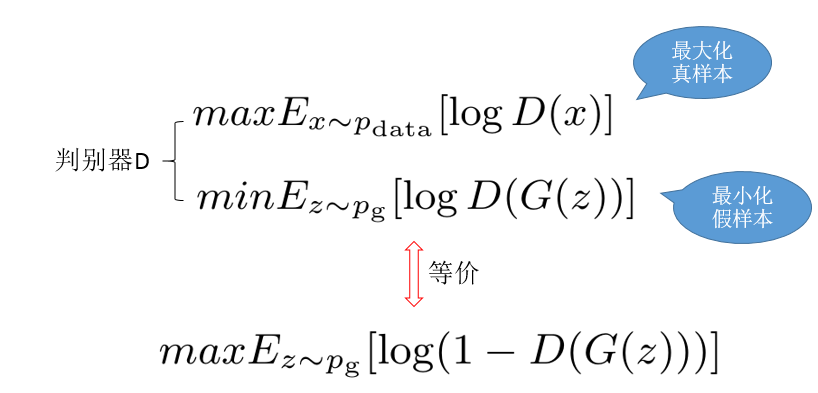
根据等价关系,合并上面两项,得到判别器目标函数:
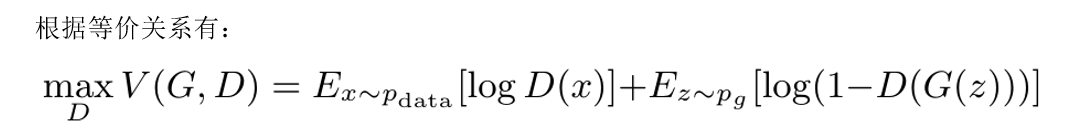
生成器目标函数
生成器的目标就是生成样本,让判别器无法区分这些样本是假的,所以它的目标函数就是如下形式:
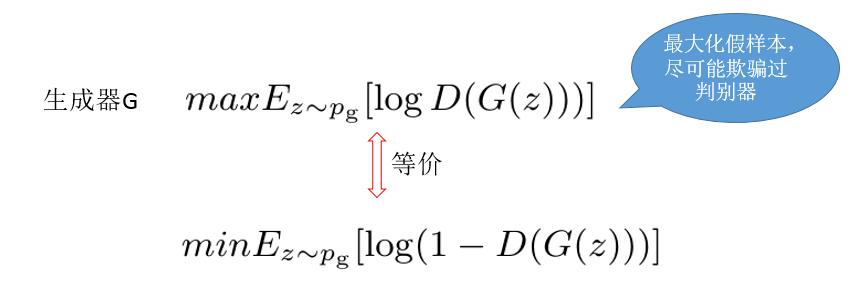
同样根据等价关系,得到生成器目标函数:
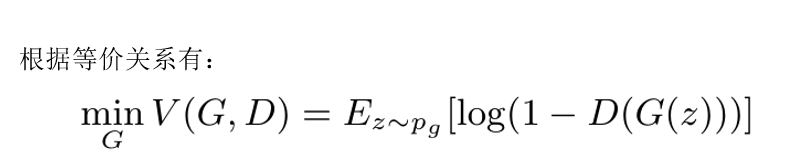
联合判别器和生成器可以得到最终的目标函数:

训练策略
- 1.随机初始化生成器G 和判别器D
- 2.交替训练生成器G 和判别器D ,直到收敛
- 2.1 训练判别器
- 从数据集中采样的真实样本
x;
- 从一个分布(均匀、正态)中采样的随机样本z;
- 通过生成器生成假样本
G(z);
- 更新判别器参数
θd,最大化D的目标函数:
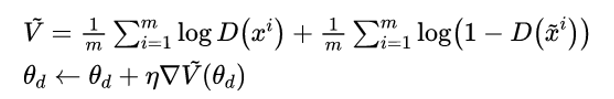
- 2.2 训练生成器
- 从一个分布(均匀、正态)中采样的随机样本
z;
- 更新生成器参数
θg,最小化G的目标函数:
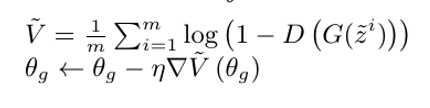
证明目标函数有解
由上面的分析,GAN的目标函数是:
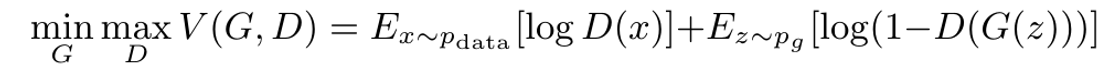
现给出如下证明:
先求判别器D的最大值,此时,生成器G固定住,值已经产生。
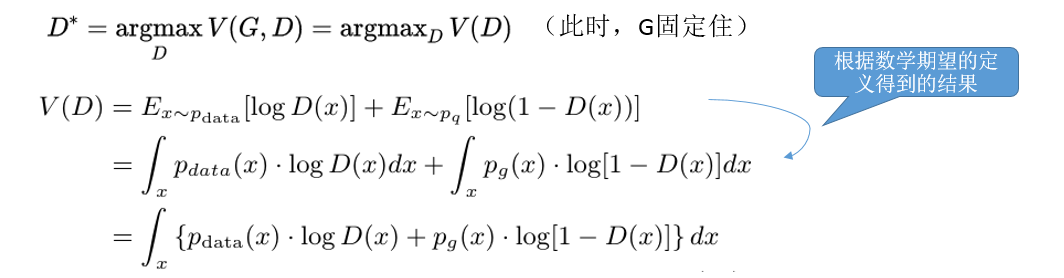
用变量替换上面的值(a,b表示概率值,范围在[0,1])

上面完整的等式是求积分后的最值,为了方便求解,我们只自求里面的值,这个结果并不影响积分的最值,所以有:

求全局极值是最优化方法的目的。对于一元二阶可导函数,求极值的一种方法是求驻点(亦称为静止点,停留点,英语:stationary point),也就是求一阶导数为零的点。如果在驻点的二阶导数为正,那么这个点就是局部最小值;如果二阶导数为负,则是局部最大值;如果为零,则还需要进一步的研究。(来源于维基百科)

根据上面求导过程,可以得出结论:
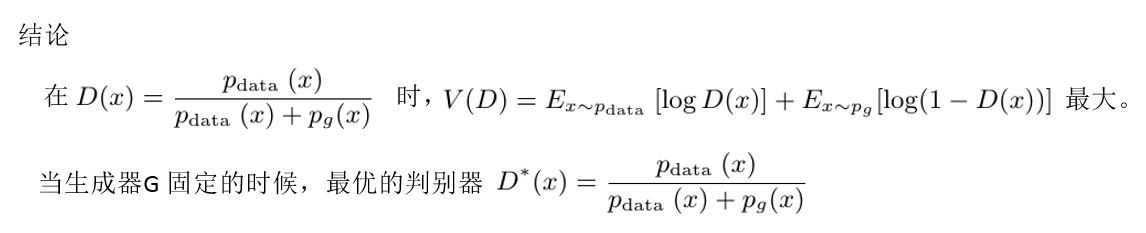
把最优的判别器D带入到GAN的目标函数:
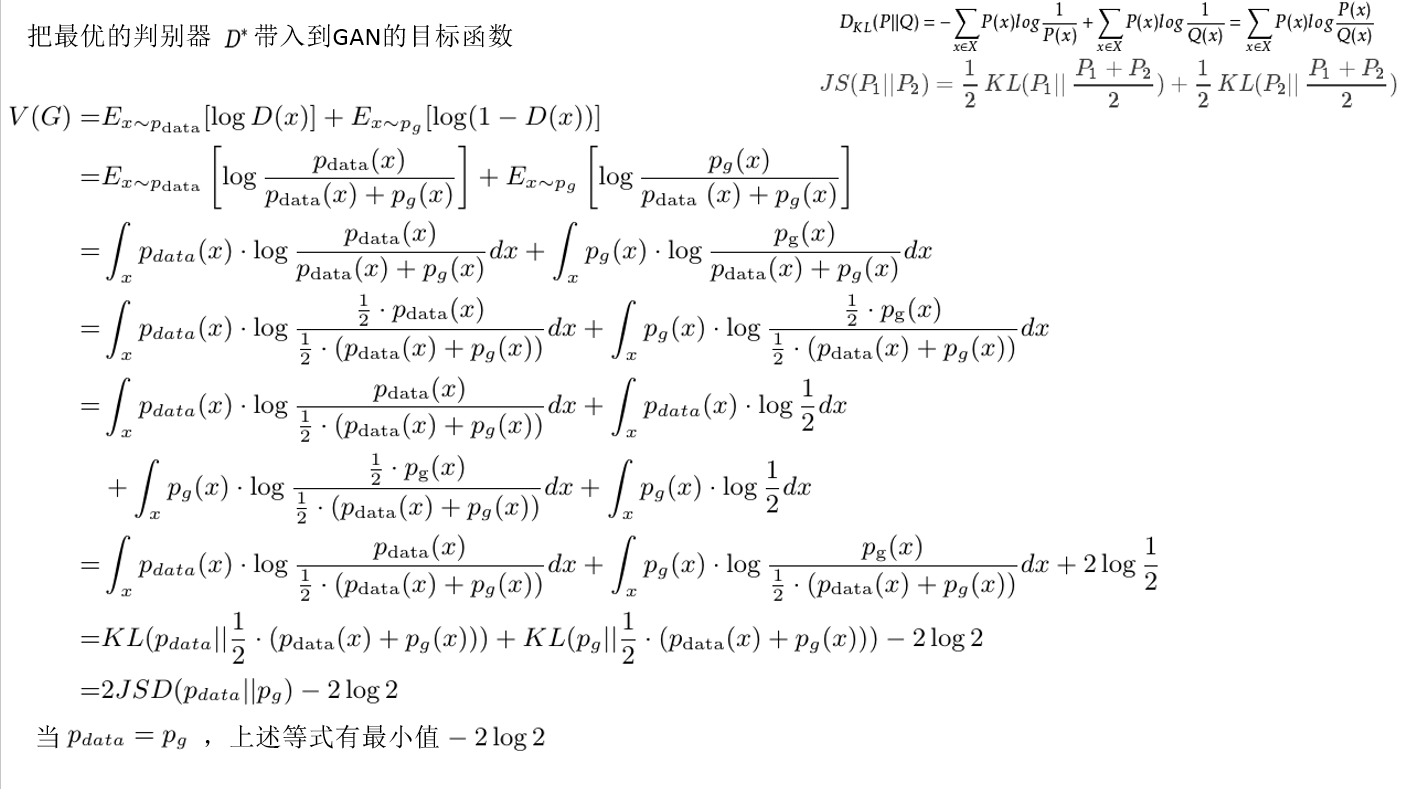
通过对生成器G公式推导,我们可以进一步得到结论:当Pdata=Pg时,V(G)有最小值,最小值是-2log2;也就是说,当生成器生成的图片分布和真实值的分布一样时,网络模型确实可以达到平衡。
参考资料:
07 Jun 2019 |
Algorithm |
这道题来自于Leetcode的第10题
题目描述:
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
’.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: “a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: “.” 表示可匹配零个或多个(’‘)任意字符(’.’)。
示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 ‘*’ 表示零个或多个,这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。
示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
方法一:递归回溯
首先,需要考虑匹配符号 * , 它会影响前面的字符,根据不同状态有:
- 如果
p[j+1] == ‘*’:
- 则有当前字符出现
0次,match(s[i],p[j+2]);
- 当前字符出现
1次,match(s[i+1],p[j+2]);
- 当前字符出现
多次,match(s[i],p[j+1]);
- 如果
p[j+1] != ‘*’:
- 那么根据当前字符处理下一个,有
match(s[i],p[j+1])。
如果觉得文字描述的不太准确的,就直接看代码吧。
递归代码:
/**
* 递归
*
* @param s 字符串
* @param p 模式串
* @return 返回结果是否匹配
*/
public boolean isMatch(String s, String p) {
if (s == null || p == null)
return false;
s = s.trim();
p = p.trim();
return match(s, p, 0, 0);
}
private boolean match(String s, String p, int sIndex, int pIndex) {
// 匹配成功
if (sIndex == s.length() && pIndex == p.length())
return true;
//字符串还没匹配完,模式串就完了,匹配失败
if (sIndex != s.length() && pIndex == p.length())
return false;
//前面出现 通配符 '*'
if (pIndex < p.length() - 1 && p.charAt(pIndex + 1) == '*') {
if ((sIndex != s.length() && s.charAt(sIndex) == p.charAt(pIndex)) || (sIndex != s.length() && p.charAt(pIndex) == '.')) {
return match(s, p, sIndex, pIndex + 2) //'*'零次,比如:ab,a*ab
|| match(s, p, sIndex + 1, pIndex + 2) //'*'一次,比如:abc,a*bc
|| match(s, p, sIndex + 1, pIndex); //'*'多次,比如:aaaa,a*
} else {
return match(s, p, sIndex, pIndex + 2); //当前不匹配, 比如:aa,c*aa
}
}
//处理 前面没有通配符 '*'
if ((sIndex != s.length() && s.charAt(sIndex) == p.charAt(pIndex)) || (sIndex != s.length() && p.charAt(pIndex) == '.')) {
return match(s, p, sIndex + 1, pIndex + 1);
}
return false;
}
方法二:动态规划
用递归实现,一般都可以转成动态规划来消除递归过程中重复计算的子问题。
动态规划最重要的是写出转移方程,这里,直接给出结果:
如果 p[j+1] == ‘*’
dp[i][j] = dp[i][j+2] || dp[i+1][j] && curMatch
(dp是状态转移表,curMatch表示当前字符是否匹配)
如果 p[j+1] != ‘*’
dp[i][j] = dp[i+1][j+1] && curMatch
这个转移方程肯定不是一下就直接看出来的,需要根据例子去不断尝试,才能找出这种规律。
因为*会影响前面的字符,
我们在从左往右计算时总是要考虑后面的字符(考虑后面是不是有*),但是后面还没有计算,还不知道结果。
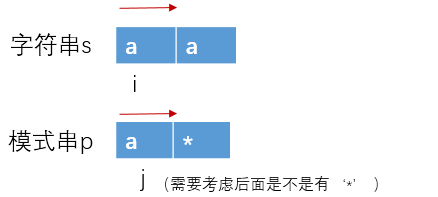
所以,我们就从后往前算,这样方便一点,因为后面此时已经计算出来了(前面写的转移方程也是从后往前的)。当然,动态规划可以从左到右,也可以从右到左。
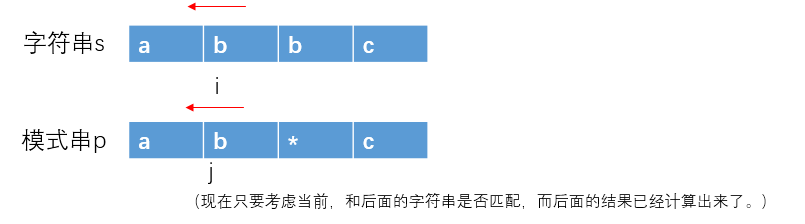
现在考虑
s[i:]表示字符串s从i(包括i)到末尾的子串;
p[j:]表示模式串p从j (包括j)到末尾的子串;在状态表中dp[i][j] 表示s[i:]和p[j:]是否匹配。
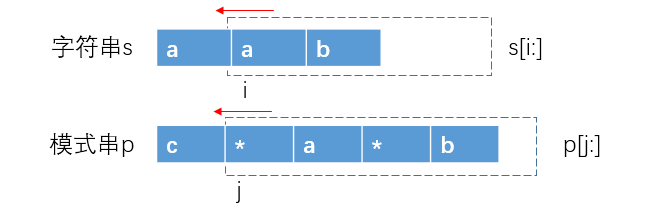
动态转移方程

动态转移方程举例说明:
` p[j+1] != ‘*’`
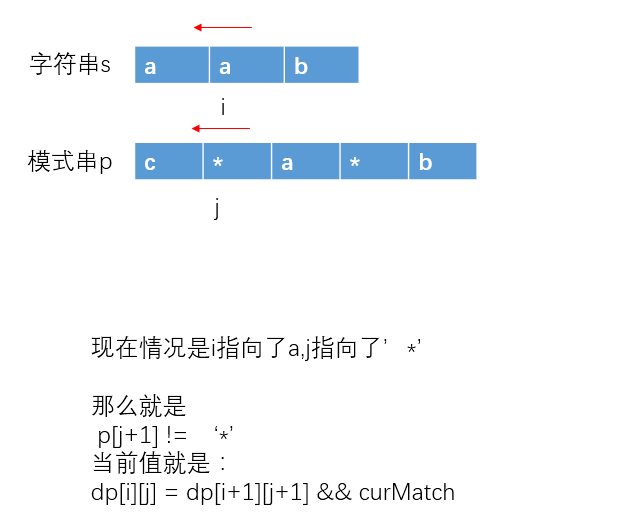
` p[j+1] == ‘*’`
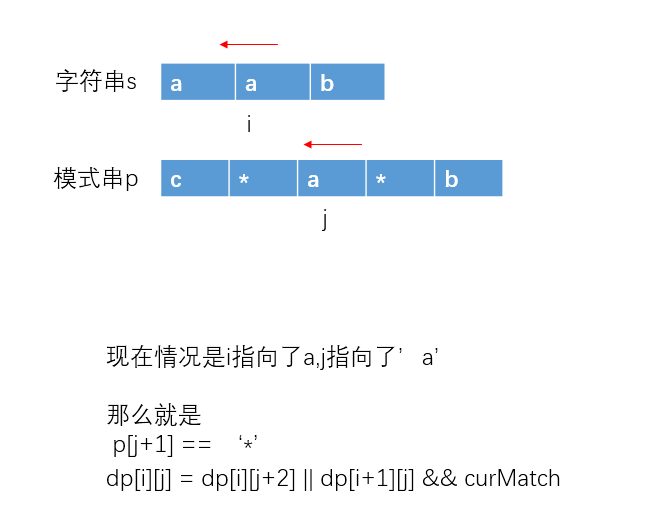
计算状态转移表
当前实例:
字符串s:"aab"
模式串p:"c*a*b"
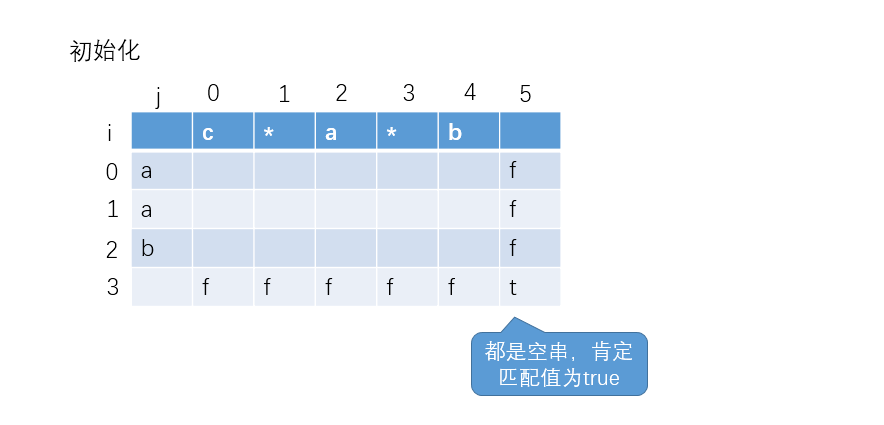
多加的一列和一行是为了方便计算,因为最后字符有+1(i+1或者j+1)的操作,可能越界。
当前实例:
字符串s:"aab"
模式串p:"c*a*b"
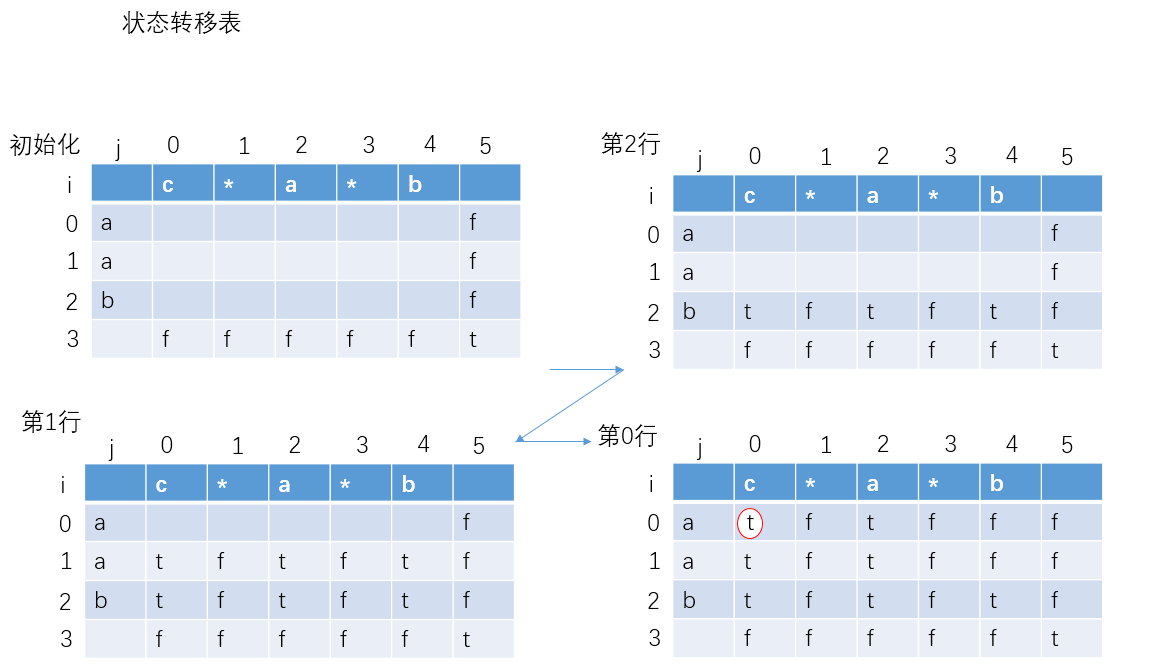
上面的实例图可以很清楚看到动态转移的过程,我们是从后往前进行计算的,所以是从第3、2、1、0行。
最后,再拿表中的例子说明一下。当i=1, j=2时,状态表情况如下:
当前实例:
字符串s:"aab"
模式串p:"c*a*b"
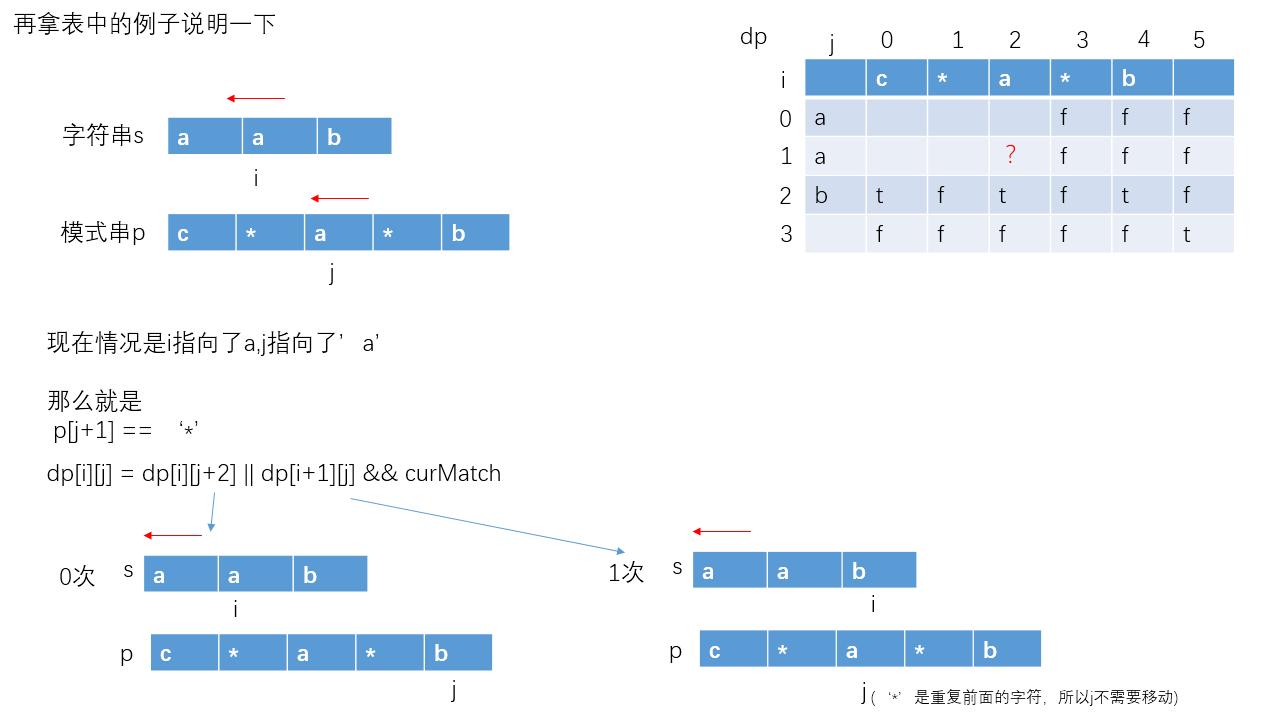
动态规划代码
/**
* 动态规划
*
* @param s 字符串
* @param p 模式串
* @return 返回结果是否匹配
*/
public boolean isMatch(String s, String p) {
//参数检查
if (s == null || p == null)
return false;
//动态规划状态转移表
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
//最后一个为true
dp[s.length()][p.length()] = true;
//初始化最后一行
for (int j = p.length() - 1; j >= 0; --j) {
if (j + 1 < p.length() && p.charAt(j + 1) == '*') {
dp[s.length()][j] = dp[s.length()][j + 2];
}//else 其他情况为false,省略了
}
//初始化最后一列, 但都为false,省略了
//计算状态转移表
for (int i = s.length() - 1; i >= 0; --i) {
for (int j = p.length() - 1; j >= 0; --j) {
boolean curMatch = s.charAt(i) == p.charAt(j) || p.charAt(j) == '.';
//对匹配符号的处理
if (j + 1 < p.length() && p.charAt(j + 1) == '*') {
dp[i][j] = dp[i][j + 2] || dp[i + 1][j] && curMatch;
} else {
dp[i][j] = dp[i + 1][j + 1] && curMatch;
}
}
}
//返回结果
return dp[0][0];
}
在状态转移表中,每次只会使用相邻的两行,所以可以使用滚动数组来节约空间。
/**
* 动态规划: 使用滚动数组节约空间
*
* @param s 字符串
* @param p 模式串
* @return 返回结果是否匹配
*/
public boolean isMatch(String s, String p) {
//参数检查
if (s == null || p == null)
return false;
//动态规划状态转移表
boolean[][] dp = new boolean[2][p.length() + 1];
//计算状态转移表
for (int i = s.length(); i >= 0; --i) {
for (int j = p.length(); j >= 0; --j) {
if (j == p.length()) {
dp[i % 2][j] = i == s.length();
}else {
boolean curMatch = i < s.length() && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.');
if (j + 1 < p.length() && p.charAt(j + 1) == '*') {
dp[i % 2][j] = dp[i % 2][j + 2] || curMatch && dp[(i + 1) % 2][j];
} else {
dp[i % 2][j] = curMatch && dp[(i + 1) % 2][j + 1];
}
}
}
}
return dp[0][0];
}
参考文献: