GAN原理
26 Jun 2019 | deep-learning |GAN(Generative Adversarial Network):生成对抗网络。
核心思想
- 判别器区分真假样本;
- 生成器欺骗判别器。
目标函数
判别器目标函数
- 判别器的目标就是区分真假样本,其实就是一个二分类,所以它的目标函数就是如下形式:
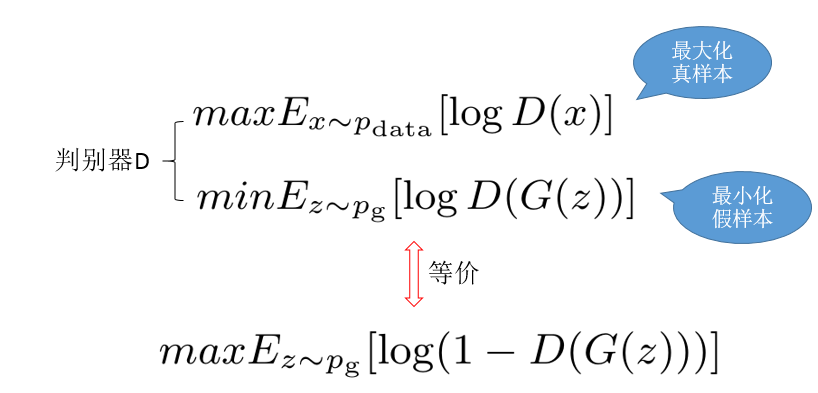
根据等价关系,合并上面两项,得到判别器目标函数:
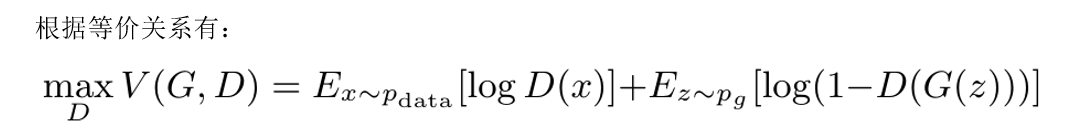
生成器目标函数
生成器的目标就是生成样本,让判别器无法区分这些样本是假的,所以它的目标函数就是如下形式:
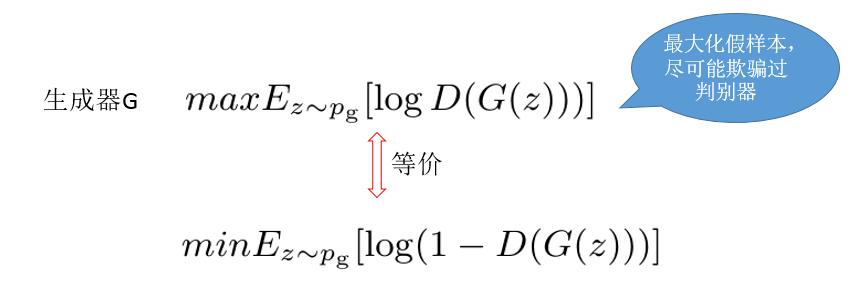
同样根据等价关系,得到生成器目标函数:
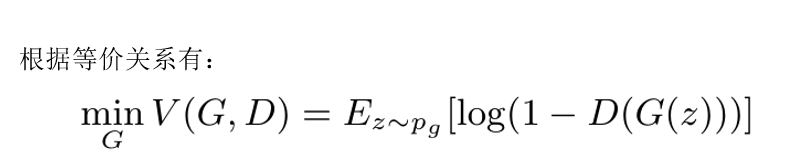
联合判别器和生成器可以得到最终的目标函数:

训练策略
- 1.随机初始化生成器G 和判别器D
- 2.交替训练生成器G 和判别器D ,直到收敛
- 2.1 训练判别器
- 从数据集中采样的真实样本
x; - 从一个分布(均匀、正态)中采样的随机样本z;
- 通过生成器生成假样本
G(z); - 更新判别器参数
θd,最大化D的目标函数: 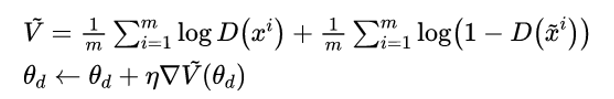
- 2.2 训练生成器
- 从一个分布(均匀、正态)中采样的随机样本
z; - 更新生成器参数
θg,最小化G的目标函数: 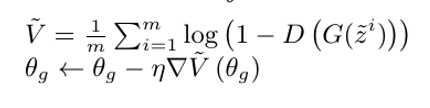
证明目标函数有解
由上面的分析,GAN的目标函数是:
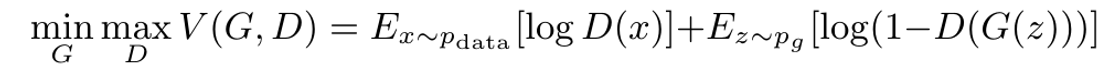
现给出如下证明:
先求判别器D的最大值,此时,生成器G固定住,值已经产生。
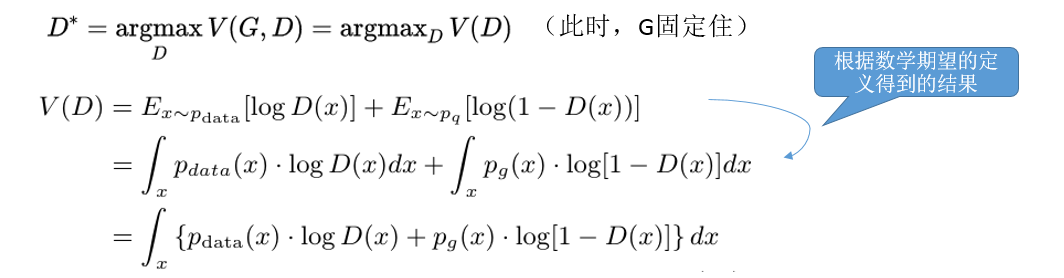
用变量替换上面的值(a,b表示概率值,范围在[0,1])

上面完整的等式是求积分后的最值,为了方便求解,我们只自求里面的值,这个结果并不影响积分的最值,所以有:

求全局极值是最优化方法的目的。对于一元二阶可导函数,求极值的一种方法是求驻点(亦称为静止点,停留点,英语:stationary point),也就是求一阶导数为零的点。如果在驻点的二阶导数为正,那么这个点就是局部最小值;如果二阶导数为负,则是局部最大值;如果为零,则还需要进一步的研究。(来源于维基百科)

根据上面求导过程,可以得出结论:
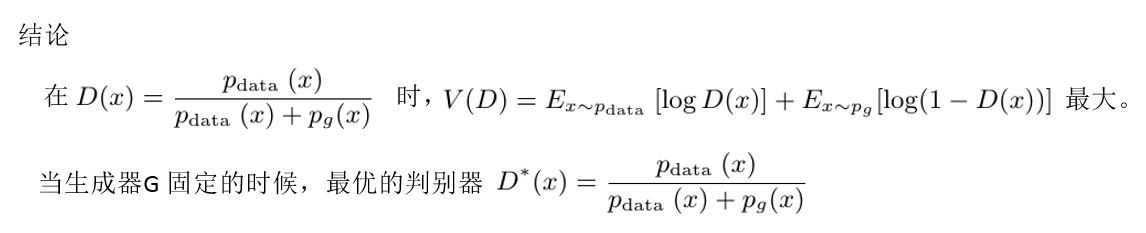
把最优的判别器D带入到GAN的目标函数:
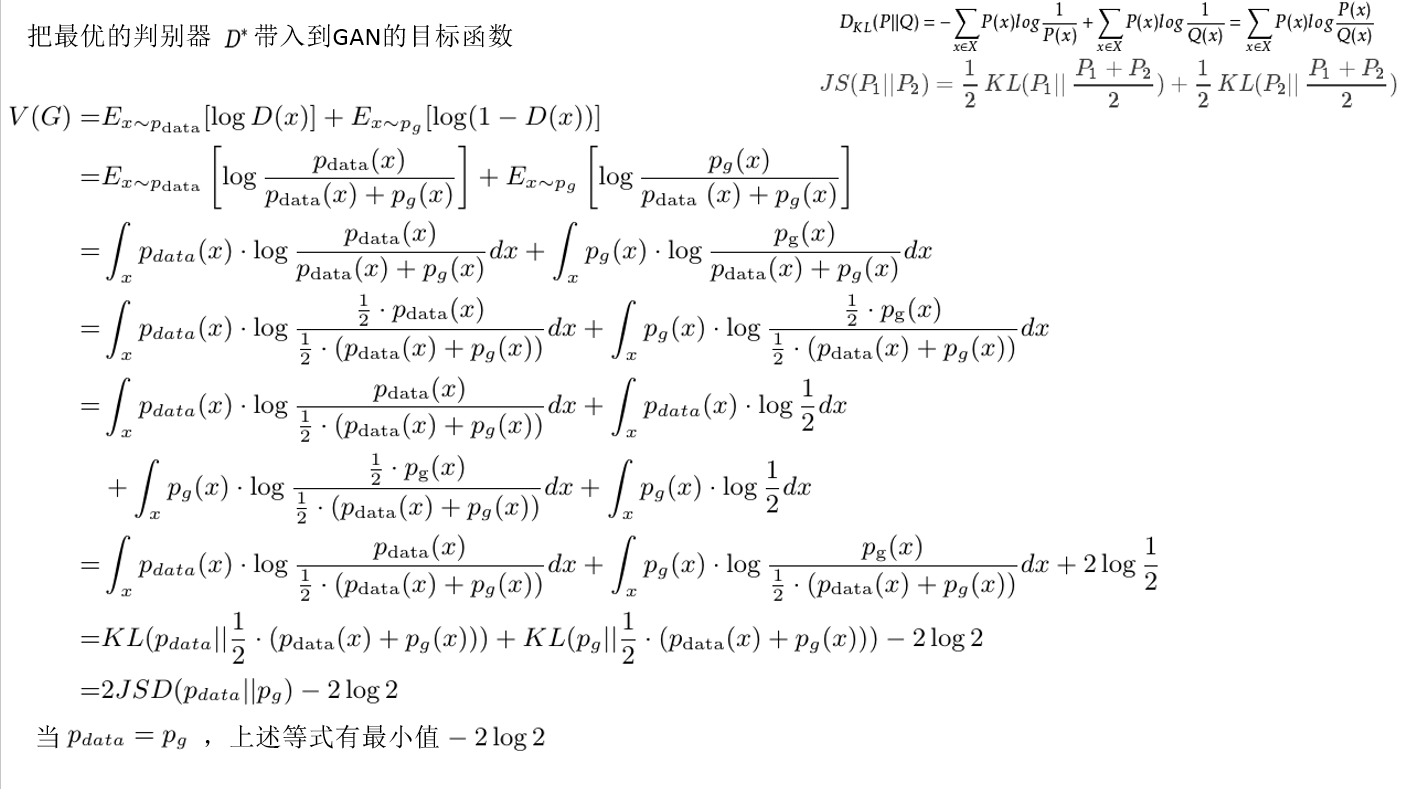
通过对生成器G公式推导,我们可以进一步得到结论:当Pdata=Pg时,V(G)有最小值,最小值是-2log2;也就是说,当生成器生成的图片分布和真实值的分布一样时,网络模型确实可以达到平衡。