Midnight

核心二元词典的加载

09 Aug 2018   |   NLP  |  

二元词典保存的是两个词之间的频次，举个栗子：

锻炼@健身 12
锻炼@其实 2
锻炼@减肥 6
有@意外 102
有@意见 128
有@意识形态 6
有@意趣 6
做@了 3454
做@争辩 6
做@事先 2

上面是一个小小的二元词典，用文本文件保存的，保存的形式是：第一个词@第二次 频率， 比如，锻炼@健身 12表示的是锻炼健身这对词语一起出现在语料中的的频率是12次。

那么我们要怎么把它加载到内存中呢？

下面的示例过程是根据HanLP中的实现来讲解的。你可以参考HanLP的核心二元词典源码。

它主要是使用两个数组来实现的:

  /**
     * 描述了词在pair中的范围，具体说来<br>
     * 给定一个词idA，从pair[start[idA]]开始的start[idA + 1] - start[idA]描述了一些接续的频次
     */
    static int start[];
    /**
     * pair[偶数n]表示key，pair[n+1]表示frequency
     */
    static int pair[];

部分示例代码：

start = new int[maxWordId + 1];
            pair = new int[total];  // total是接续的个数*2
            int offset = 0;

            for (int i = 0; i < maxWordId; ++i)
            {
                TreeMap<Integer, Integer> bMap = map.get(i);//获取第一个词
                if (bMap != null)
                {
                    for (Map.Entry<Integer, Integer> entry : bMap.entrySet())
                    {
                        int index = offset << 1;
                        pair[index] = entry.getKey();//保存第二个词的id
                        pair[index + 1] = entry.getValue();//保存两个词的频率
                        ++offset;
                    }
                }
                start[i + 1] = offset;
            }

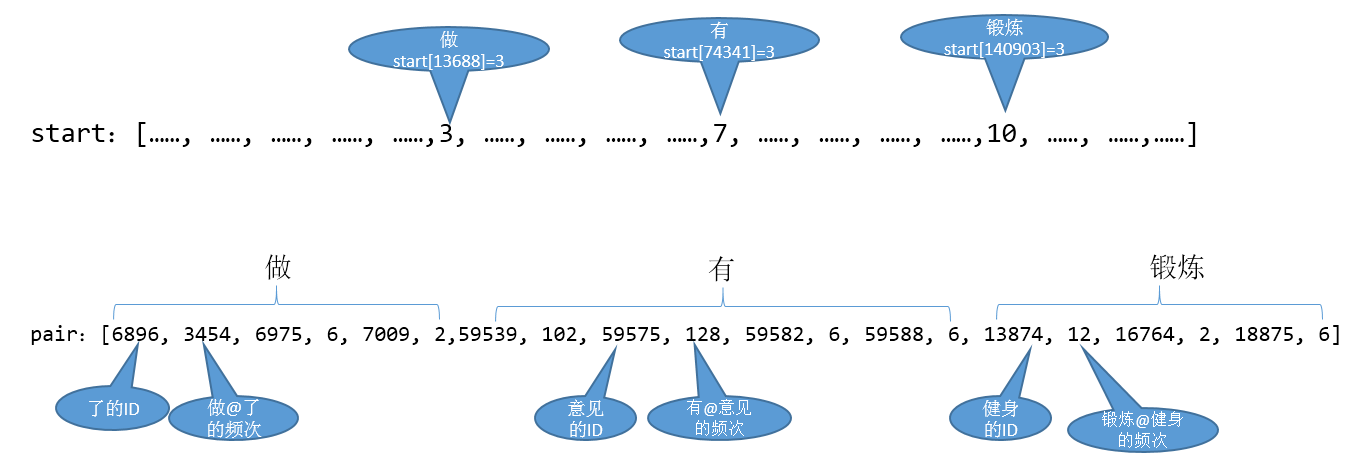
仍然以上面的小的二元词典为例，最终的数组形式是： image

要查找一个二元词频的时候，可以直接使用二分查找：

public class Mytest {
    public static void main(String[] args){
        int[] a = {6896, 3454, 6975, 6, 7009, 2,
                   59539, 102, 59575, 128, 59582, 6, 59588, 6,
                   13874, 12, 16764, 2, 18875, 6};

       int index = binarySearch(a,0,7,59575); // 查找“有意见”的词频
        
       System.out.print(pair[index+1]);

    }


    /**
     * 二分搜索，由于二元接续前一个词固定时，后一个词比较少，所以二分也能取得很高的性能
     * @param a 目标数组
     * @param fromIndex 开始下标
     * @param length 长度
     * @param key 词的id
     * @return 共现频次
     */
    private static int binarySearch(int[] a, int fromIndex, int length, int key)
    {
        int low = fromIndex;
        int high = fromIndex + length - 1;

        while (low <= high)
        {
            int mid = (low + high) >>> 1;
            int midVal = a[mid << 1];

            if (midVal < key)
                low = mid + 1;
            else if (midVal > key)
                high = mid - 1;
            else
                return mid; // key found
        }
        return -(low + 1);  // key not found.
    }
}

Related Posts...