权重初始化
24 Mar 2018 | deep-learning |权重初始化
选择一个好的初始值可以让神经网络达到最优,也可以让网络更快的收敛。文件来源于udacity
测试权重
数据集
为了展示不同权重的执行情况,我们需要采用相同的数据集和神经网络上面。首先,我们使用的数据集是 MNIST dataset ,该数据集的输入都是经过归一化处理后的数据,数据值在(0,1)。
%matplotlib inline
import tensorflow as tf
import helper
from tensorflow.examples.tutorials.mnist import input_data
print('Getting MNIST Dataset...')
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
print('Data Extracted.')
Getting MNIST Dataset...
Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
Data Extracted.
神经网络
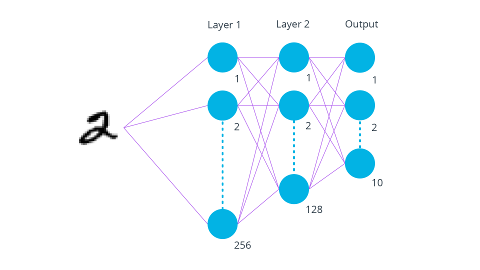
对于神经网络,我们的层数是3层,RELU作为激活函数,Adam作为优化器。
# 保存每一层权重的形状
layer_1_weight_shape = (mnist.train.images.shape[1], 256)
layer_2_weight_shape = (256, 128)
layer_3_weight_shape = (128, mnist.train.labels.shape[1])
初始化权重
首先,让我们初始化一些权重吧!
全为0或者1
或许你会认为把权重设置为0或者1是比较好的方式,但是,事实并不是这样的。我们来比较一下权重全为0或者全为1时的损失吧。辅助函数helper.compare_init_weights将会把这两种不同的权重初始值运行在神经网络上面两个周期。它会对第一个100 batches绘制出损失,并且打印出两个周期(大约有860个 batches)后的输出状态。为了判断哪一个权重初始值在开始的时候执行的更好,我们绘制了第一个100 batches。
all_zero_weights = [
tf.Variable(tf.zeros(layer_1_weight_shape)),
tf.Variable(tf.zeros(layer_2_weight_shape)),
tf.Variable(tf.zeros(layer_3_weight_shape))
]
all_one_weights = [
tf.Variable(tf.ones(layer_1_weight_shape)),
tf.Variable(tf.ones(layer_2_weight_shape)),
tf.Variable(tf.ones(layer_3_weight_shape))
]
helper.compare_init_weights(
mnist,
'All Zeros vs All Ones',
[
(all_zero_weights, 'All Zeros'),
(all_one_weights, 'All Ones')])
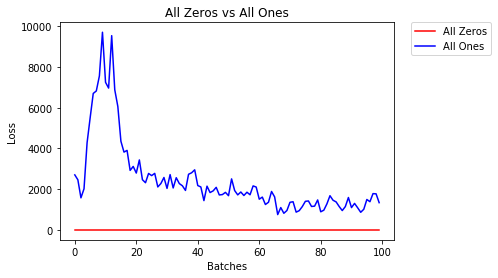
After 858 Batches (2 Epochs):
Validation Accuracy
11.260% -- All Zeros
9.580% -- All Ones
Loss
2.306 -- All Zeros
197.818 -- All Ones
如你所见,对于全0或者全1的精确度近似于猜测,都是10%左右。为了避免权重值相同,我们需要随机选取不同的权重初始值,一个好的方式是从均匀分布中进行采样。
均匀分布是等概率的从一组数据中选取值。我们将要从连续的分布中选取值,所以,选取到相同的值得概率比较低。
我们将使用tensorflow的tf.random_uniform函数从均匀分布中选取值。
tf.random_uniform(shape, minval=0, maxval=None, dtype=tf.float32, seed=None, name=None)从均匀分布中输出随机值,值得范围在[minval, maxval)之间,包括下限,不包括上限。
我们可以使用直方图对输出值进行可视化
# 从[-3,3)随机选择1000个值
helper.hist_dist('Random Uniform (minval=-3, maxval=3)', tf.random_uniform([1000], -3, 3))
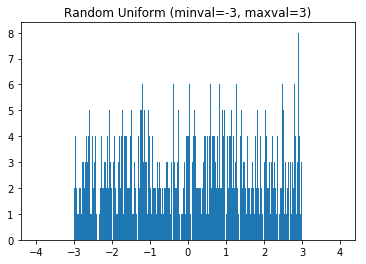
均匀分布
我们使用均匀分布来初始化权重吧,看看结果如何呢?
# f.random_uniform 的默认值是 minval=0 and maxval=1
basline_weights = [
tf.Variable(tf.random_uniform(layer_1_weight_shape)),
tf.Variable(tf.random_uniform(layer_2_weight_shape)),
tf.Variable(tf.random_uniform(layer_3_weight_shape))
]
helper.compare_init_weights(
mnist,
'Baseline',
[(basline_weights, 'tf.random_uniform [0, 1)')])
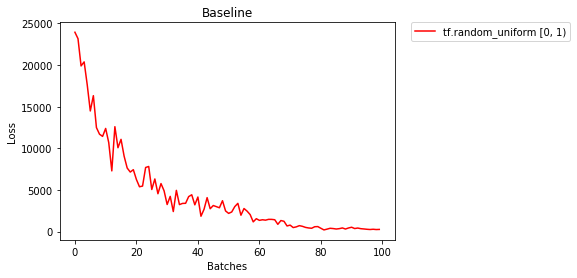
After 858 Batches (2 Epochs):
Validation Accuracy
76.620% -- tf.random_uniform [0, 1)
Loss
22.214 -- tf.random_uniform [0, 1)
图中显示损失在逐渐下降,表明我们在朝着正确的方向前进。
设置权重的一般规则
设置权重的一般规则是接近0但是又不能太小了,一般是在[-y, y]之间,其中$y=1/\sqrt{n}$(n是输入神经元的个数)
uniform_neg1to1_weights = [
tf.Variable(tf.random_uniform(layer_1_weight_shape, -1, 1)),
tf.Variable(tf.random_uniform(layer_2_weight_shape, -1, 1)),
tf.Variable(tf.random_uniform(layer_3_weight_shape, -1, 1))
]
helper.compare_init_weights(
mnist,
'[0, 1) vs [-1, 1)',
[
(basline_weights, 'tf.random_uniform [0, 1)'),
(uniform_neg1to1_weights, 'tf.random_uniform [-1, 1)')])
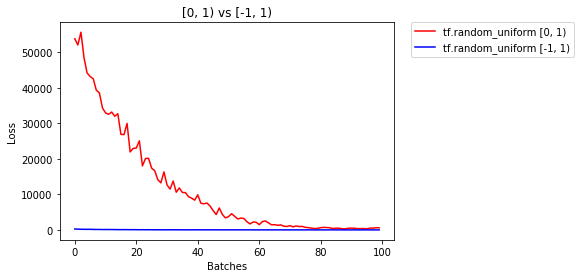
After 858 Batches (2 Epochs):
Validation Accuracy
73.220% -- tf.random_uniform [0, 1)
90.940% -- tf.random_uniform [-1, 1)
Loss
20.096 -- tf.random_uniform [0, 1)
6.447 -- tf.random_uniform [-1, 1)
太小
我们来比较一下 Let’s compare [-0.1, 0.1), [-0.01, 0.01), 和[-0.001, 0.001),看看多小才算小呢?
uniform_neg01to01_weights = [
tf.Variable(tf.random_uniform(layer_1_weight_shape, -0.1, 0.1)),
tf.Variable(tf.random_uniform(layer_2_weight_shape, -0.1, 0.1)),
tf.Variable(tf.random_uniform(layer_3_weight_shape, -0.1, 0.1))
]
uniform_neg001to001_weights = [
tf.Variable(tf.random_uniform(layer_1_weight_shape, -0.01, 0.01)),
tf.Variable(tf.random_uniform(layer_2_weight_shape, -0.01, 0.01)),
tf.Variable(tf.random_uniform(layer_3_weight_shape, -0.01, 0.01))
]
uniform_neg0001to0001_weights = [
tf.Variable(tf.random_uniform(layer_1_weight_shape, -0.001, 0.001)),
tf.Variable(tf.random_uniform(layer_2_weight_shape, -0.001, 0.001)),
tf.Variable(tf.random_uniform(layer_3_weight_shape, -0.001, 0.001))
]
helper.compare_init_weights(
mnist,
'[-1, 1) vs [-0.1, 0.1) vs [-0.01, 0.01) vs [-0.001, 0.001)',
[
(uniform_neg1to1_weights, '[-1, 1)'),
(uniform_neg01to01_weights, '[-0.1, 0.1)'),
(uniform_neg001to001_weights, '[-0.01, 0.01)'),
(uniform_neg0001to0001_weights, '[-0.001, 0.001)')],
plot_n_batches=None)
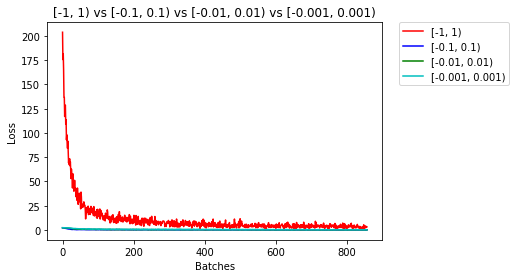
After 858 Batches (2 Epochs):
Validation Accuracy
90.000% -- [-1, 1)
97.160% -- [-0.1, 0.1)
95.680% -- [-0.01, 0.01)
93.520% -- [-0.001, 0.001)
Loss
3.161 -- [-1, 1)
0.050 -- [-0.1, 0.1)
0.134 -- [-0.01, 0.01)
0.169 -- [-0.001, 0.001)
在[-0.01, 0.01)之间或者更小的值,精度开始下降了,接下来比较一下[-0.1, 0.1)和一般的规则
import numpy as np
general_rule_weights = [
tf.Variable(tf.random_uniform(layer_1_weight_shape, -1/np.sqrt(layer_1_weight_shape[0]), 1/np.sqrt(layer_1_weight_shape[0]))),
tf.Variable(tf.random_uniform(layer_2_weight_shape, -1/np.sqrt(layer_2_weight_shape[0]), 1/np.sqrt(layer_2_weight_shape[0]))),
tf.Variable(tf.random_uniform(layer_3_weight_shape, -1/np.sqrt(layer_3_weight_shape[0]), 1/np.sqrt(layer_3_weight_shape[0])))
]
helper.compare_init_weights(
mnist,
'[-0.1, 0.1) vs General Rule',
[
(uniform_neg01to01_weights, '[-0.1, 0.1)'),
(general_rule_weights, 'General Rule')],
plot_n_batches=None)
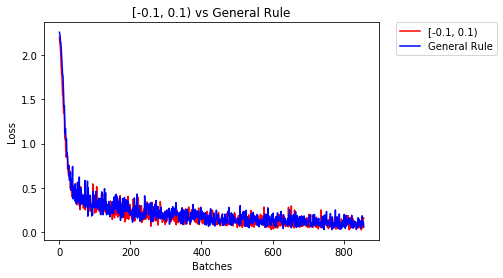
After 858 Batches (2 Epochs):
Validation Accuracy
97.120% -- [-0.1, 0.1)
96.860% -- General Rule
Loss
0.161 -- [-0.1, 0.1)
0.062 -- General Rule
上面的结果是比较接近的。
因为均匀分布式等概率选取值的,那么如果我们选择一个有更高的概率选择靠近0的值的概率分布会怎样呢?让我们来试试正态分布吧!
正态分布
与均匀分布不同的是, 正态分布 有更高的概率去选择接近它的均值的值。 我们可以使用TensorFlow的 tf.random_normal 函数来使用正态分布,同样可以使用等高图进行可视化。
tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
从正态分布中输出随机值
helper.hist_dist('Random Normal (mean=0.0, stddev=1.0)', tf.random_normal([1000]))
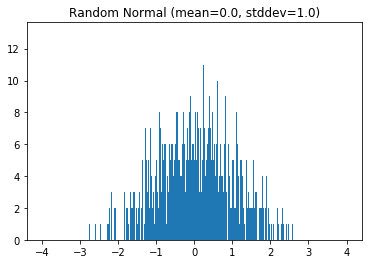
让我们来比较一下正态分布和均匀分布吧。
normal_01_weights = [
tf.Variable(tf.random_normal(layer_1_weight_shape, stddev=0.1)),
tf.Variable(tf.random_normal(layer_2_weight_shape, stddev=0.1)),
tf.Variable(tf.random_normal(layer_3_weight_shape, stddev=0.1))
]
helper.compare_init_weights(
mnist,
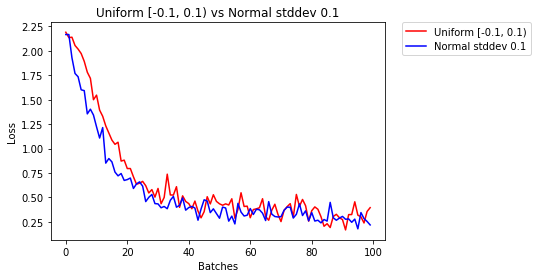
'Uniform [-0.1, 0.1) vs Normal stddev 0.1',
[
(uniform_neg01to01_weights, 'Uniform [-0.1, 0.1)'),
(normal_01_weights, 'Normal stddev 0.1')])
After 858 Batches (2 Epochs):
Validation Accuracy
97.200% -- Uniform [-0.1, 0.1)
97.400% -- Normal stddev 0.1
Loss
0.106 -- Uniform [-0.1, 0.1)
0.120 -- Normal stddev 0.1
上面的结果是相似的。接下来我们想更接近0,丢弃那些远离标准差的值。这样的分布函数叫做截断的正态分布。
截断的正态分布
tf.truncated_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
从截断的正态分布中输出随机值
这个函数在随机选取值时与正态分布时类似的额,只是当选到的值是远离均值2个标准差时会丢弃重新选择。
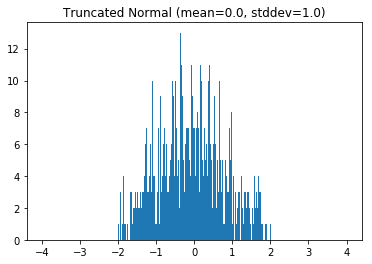
helper.hist_dist('Truncated Normal (mean=0.0, stddev=1.0)', tf.truncated_normal([1000]))
trunc_normal_01_weights = [
tf.Variable(tf.truncated_normal(layer_1_weight_shape, stddev=0.1)),
tf.Variable(tf.truncated_normal(layer_2_weight_shape, stddev=0.1)),
tf.Variable(tf.truncated_normal(layer_3_weight_shape, stddev=0.1))
]
helper.compare_init_weights(
mnist,
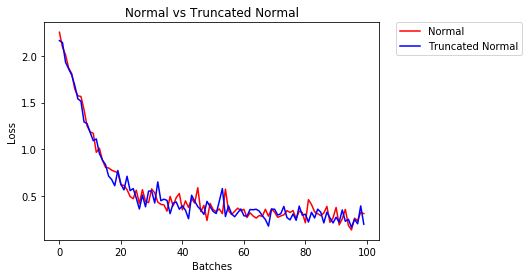
'Normal vs Truncated Normal',
[
(normal_01_weights, 'Normal'),
(trunc_normal_01_weights, 'Truncated Normal')])
After 858 Batches (2 Epochs):
Validation Accuracy
96.780% -- Normal
97.140% -- Truncated Normal
Loss
0.032 -- Normal
0.124 -- Truncated Normal
上面的结果似乎差异并不大,但是那是因为我们使用的神经网络太小了。一个更大的神经网络在正态分布中选取值时有更大的概率选取偏离2个标准差的值。 我们已经做了多组实验了,最后看看当初选择的权重和最后选择的权重的区别吧!
helper.compare_init_weights(
mnist,
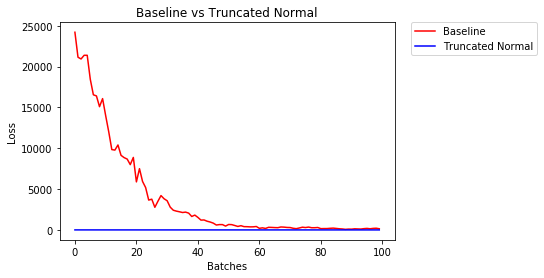
'Baseline vs Truncated Normal',
[
(basline_weights, 'Baseline'),
(trunc_normal_01_weights, 'Truncated Normal')])
After 858 Batches (2 Epochs):
Validation Accuracy
79.500% -- Baseline
97.060% -- Truncated Normal
Loss
12.562 -- Baseline
0.101 -- Truncated Normal
上面的差异是巨大的,截断的正态分布的精度比一般的分布要高得多。 近年来,新的权重处理方法不断被提出,在此列举一些对神经网络领域影响较大的论文: