反向传播数学推导与代码实现

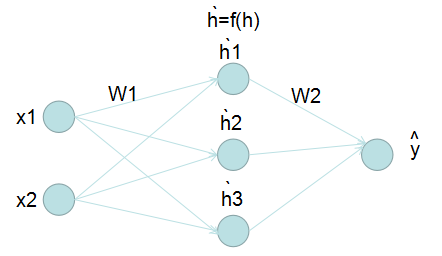
18 Mar 2018 | deep-learning |

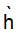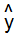下面是简单的前向传播神经网络，其中x1 x2是输入，h是线性组合的值，f(h)是通过激活函数后激活的值(也就是h上面有一撇),输出是(用y上面有一个尖尖来表示输出)，W1是输入层到隐藏层之间的权重值，W2是隐藏层到输出层之间的权重值。

神经网络的前向传播如下公式所示，f()是激活函数，比如sigmoid、ReLU、tanh、softmax等，x是输入，w是权重，b是偏差

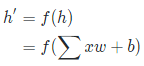
我们用如下公式来表示误差，y是给定的目标值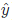，是神经网络计算出来的值：

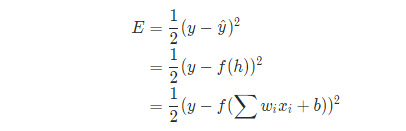
现在，我们通过梯度下降的方法来反向求权重的更新值，通过改变权重w来减小误差，权重是在梯度的相反方向，在微积分中我们知道有如下关系：

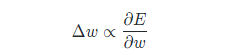
那么权重的更新就是：

首先，来求W2的权重更新值,对等式的偏微分进行展开，则有：

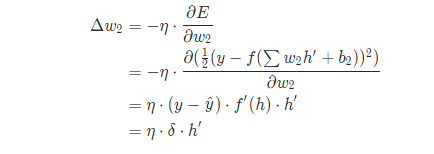
上面公式中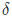是误差项（此时表示输出层的误差项），y - 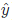是输出误差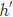，是隐藏层的值（即通过激活函数激活后的值），激活函数 f(h)的导函数是，我们把这个导函数称做输出的梯度。

接着我们来求w1的权重更新值，对w1求导我们需要利用求导的链式法则。

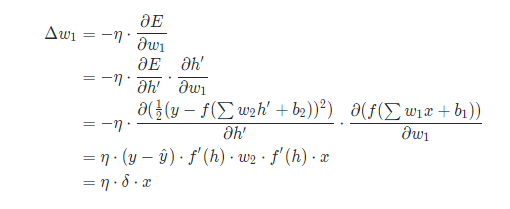上面公式中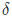任然表示是误差项（此时表示隐藏层的的误差项），x表示输入层的值。

我们可以进一步提取公式中的有效信息：

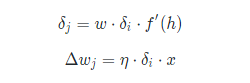
用语言来表达的话就是：

当前层的误差项等于当前层与下一层之间的权重乘以下一层的误差项乘以当前层激活函数的导数值；当前层与下一层之间的权重值更新等于学习率乘以下一层的误差项乘以当前层的激活值。

通过上面的推导，我们就可以对权重值进行更新了，比如，我要更新w11的值，就可以表示为：

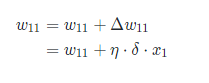
反向传播实例 1

import numpy as np


def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))
    
def sigmoid_prim(x):
    """
    Calculate sigmoid
    """
    return sigmoid(x) * (1 - sigmoid(x))

x = np.array([0.5, 0.1, -0.2])
target = 0.6
learnrate = 0.5

weights_input_hidden = np.array([[0.5, -0.6],
                                 [0.1, -0.2],
                                 [0.1, 0.7]])

weights_hidden_output = np.array([0.1, -0.3])

## Forward pass
hidden_layer_input = np.dot(x, weights_input_hidden)
hidden_layer_output = sigmoid(hidden_layer_input)

output_layer_in = np.dot(hidden_layer_output, weights_hidden_output)

output = sigmoid(output_layer_in)

## Backwards pass
## TODO: Calculate output error
error = target - output

# TODO: Calculate error term for output layer
output_error_term = error * sigmoid_prim(output_layer_in)
print(output_error_term)
print(weights_hidden_output)
# TODO: Calculate error term for hidden layer
hidden_error = np.dot(output_error_term, weights_hidden_output)
hidden_error_term = hidden_error  * sigmoid_prim(hidden_layer_input)
print("hidden_error_term:" ,hidden_error_term)
print("                  ",x[:,None])
# TODO: Calculate change in weights for hidden layer to output layer
delta_w_h_o = learnrate * output_error_term * hidden_layer_output
print("delta_w_h_o:",delta_w_h_o)
# TODO: Calculate change in weights for input layer to hidden layer
delta_w_i_h = learnrate * x[:,None] * hidden_error_term  

print('Change in weights for hidden layer to output layer:')
print(delta_w_h_o)
print('Change in weights for input layer to hidden layer:')
print(delta_w_i_h)

反向传播实例 2

import numpy as np
from data_prep import features, targets, features_test, targets_test #data import

np.random.seed(21)

def sigmoid(x):
    """
    Calculate sigmoid
    """
    return 1 / (1 + np.exp(-x))
def sigmoid_prime(x):
    """
    Calculate sigmoid
    """
    return sigmoid(x) * (1 - sigmoid(x))

# Hyperparameters
n_hidden = 2  # number of hidden units
epochs = 900
learnrate = 0.005

n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights_input_hidden = np.random.normal(scale=1 / n_features ** .5,
                                        size=(n_features, n_hidden))
weights_hidden_output = np.random.normal(scale=1 / n_features ** .5,
                                         size=n_hidden)

for e in range(epochs):
    del_w_input_hidden = np.zeros(weights_input_hidden.shape)
    del_w_hidden_output = np.zeros(weights_hidden_output.shape)
    for x, y in zip(features.values, targets):
        ## Forward pass ##
        # TODO: Calculate the output
        hidden_input = np.dot(x,weights_input_hidden)
        hidden_output = sigmoid(hidden_input)
        o_input = np.dot(hidden_output,weights_hidden_output)
        output = sigmoid(o_input)

        ## Backward pass ##
        # TODO: Calculate the network's prediction error
        error = y - output

        # TODO: Calculate error term for the output unit
        output_error_term = error * sigmoid_prime(o_input)

        ## propagate errors to hidden layer

        # TODO: Calculate the hidden layer's contribution to the error
        hidden_error = np.dot(output_error_term , weights_hidden_output)
        
        # TODO: Calculate the error term for the hidden layer
        hidden_error_term = hidden_error * sigmoid_prime(hidden_input)
        
        # TODO: Update the change in weights
        del_w_hidden_output += output_error_term * hidden_output
        del_w_input_hidden += hidden_error_term * x[:,None] 

    # TODO: Update weights
    weights_input_hidden += learnrate * del_w_input_hidden / n_records
    weights_hidden_output += learnrate * del_w_hidden_output / n_records

    # Printing out the mean square error on the training set
    if e % (epochs / 10) == 0:
        hidden_output = sigmoid(np.dot(x, weights_input_hidden))
        out = sigmoid(np.dot(hidden_output,
                             weights_hidden_output))
        loss = np.mean((out - targets) ** 2)

        if last_loss and last_loss < loss:
            print("Train loss: ", loss, "  WARNING - Loss Increasing")
        else:
            print("Train loss: ", loss)
        last_loss = loss

# Calculate accuracy on test data
hidden = sigmoid(np.dot(features_test, weights_input_hidden))
out = sigmoid(np.dot(hidden, weights_hidden_output))
predictions = out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))

Midnight